「提高 - 85」Tarjan 算法与无向图连通性

想象一个信息网络，我们需要当一个节点或一条边被破坏以后，要求剩余的节点依然保持连通，这是本节我们将研究的内容。

边双连通图

定义

tip

一张无向连通图，若删掉任意一条边，剩余的点依然保持连通，则称它为 “边双连通图”。

即边双连通图为不存在桥的无向连通图。

边双连通判定定理

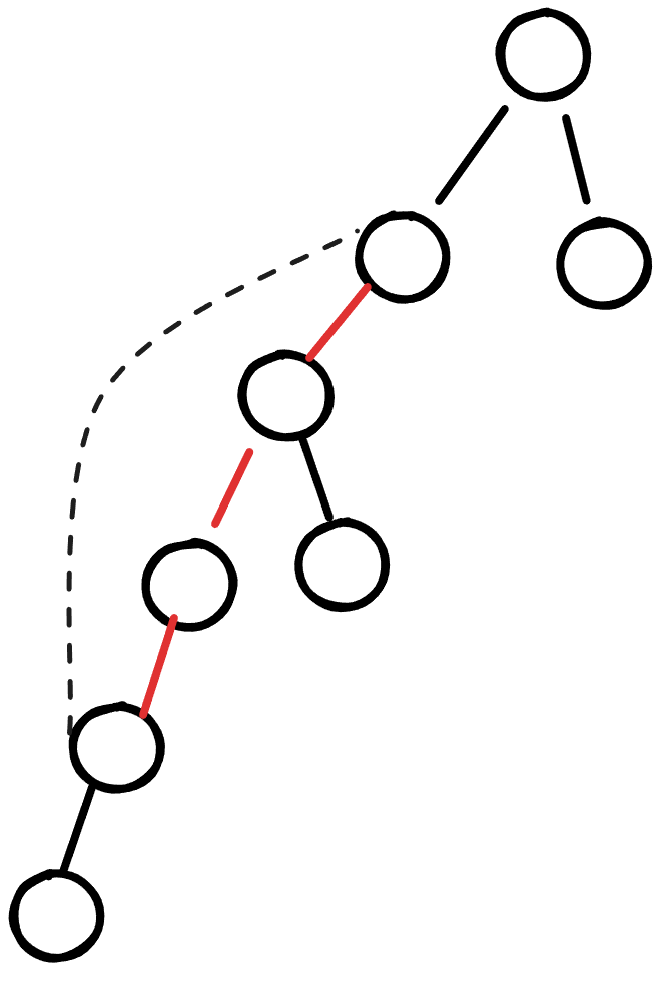
在上面的图中，因为回边的存在，那么红色的三条边都不是割边，这三条边任意删掉一条，剩下的点依然保持连通。

important

一张无向连通图是 ”边双连通图“，当且仅当任意一条边都包含在至少一个简单环中。

证明

充分性

任意一条边都包含在至少一个简单环中，意味着任意两点之间至少有两条路径，那么，无论我们删掉哪条边，剩余的点依然保持连通。

必要性

若图是边双连通图，那么对于任意一条边 $AB$，删掉边 $AB$ 之后，$A$ 和 $B$ 依然保持连通，$A$、$B$ 之间存在另一条路径，加上删掉的边 $AB$，那么 $A$ 和 $B$ 位于一个简单环中。

边双连通分量

tip

无向图的极大边双连通子图被称为”边双连通分量“，简记为 ”e-DCC“（edge double connected component）。

这里，极大的意思是在一个局部，子图不能更大。若 $G^{'}$ 是一个极大边双连通子图，意味着不存在边双连通子图 $G^{a}$，满足 $G^{'}$ 是 $G^{a}$ 的子图，但两者不相等。

边双连通分量的求法

我们求出无向图中所有的割边，删掉割边以后，无向图便会分为若干个连通块，每个连通块内不存在割边，是一个”边连通分量“。 具体实现步骤：

• 用 Tarjan 算法标记出所有的割边。
• 对整个无向图执行一次深度优先遍历，遍历的时候不访问割边，由此划分出每个连通块。

int c[SIZE], dcc;

void dfs(int x) {
  c[x] = dcc;
  for (int i = head[x]; i; i = Next[i]) {
    int y = ver[i];
    if (c[y] || bridge[i]) continue;
    dfs (y) ;
  }
}

// 这里的代码放在主函数执行了 tarjan 之后
for (int i = 1; i <= n; i++) 
  if (!c[i]) {
    ++dcc;
    dfs(i)
  }

e-DCC 的缩点

tip

把每个 e-DCC 看作一个节点，把桥边 $(x, y)$ 看作连接编号为 $c[x]$ 和 $c[y]$ 的 e-DCC 对应节点的无向边，会产生一颗树（若原来的图不连通，则产生一颗森林）。这种把 e-DCC 收缩为一个节点的方法就称为 “缩点”。

int hc[SIZE], vc[SIZE * 2], nc[SIZE * 2], nc[SIZE * 2], tc;

void add_c(int x, int y) {
  vc[++tc] = y, nc[tc] = hc[x], hc[x] = tc;
}

// 下面的代码放在主函数求 e-DCC 之后
tc = 1;
for (int i = 2; i <= tot; i++) {
  int x = ver[i ^ 1], y = ver[i];
  if (c[x] == c[y]) continue;
  add_c(c[x], c[y]);
} 

点双连通图

定义

tip

一张无向连通图，若删掉任意一点和与之相连的边，剩余的点依然保持连通，则称它为 ”点双连通图“。

即不存在割点的图即为 "点双连通图"。

点双连通判定定理

important

一张无向连通图是 ”点双连通图“，当且仅当满足下列两个条件之一：

• 图的顶点数不超过 2。
• 图中任意两点都同时包含在至少一个简单环（只有第一个与最后一个顶点相同的回路）中。

证明

若图的顶点数不超过 $2$，定理显然成立。

充分性

任意两点 $x$、$y$ 均包含在至少一个简单环中，则 $x$、$y$ 之间至少有两条不相交的路径。无论删掉哪个节点， 最多影响 $x$、$y$ 之间路径的一条，故 $x$、$y$ 均能通过两条路径之一相连。图中不存在割点，为点双连通图。

必要性

假设图为 ”点双连通图“，且存在两点 $x$、$y$ 不在简单环中。

1. 若 $x$、$y$ 之间仅存在 1 条简单路径，那么路径上最少有一个割点，与 “点双连通”矛盾。

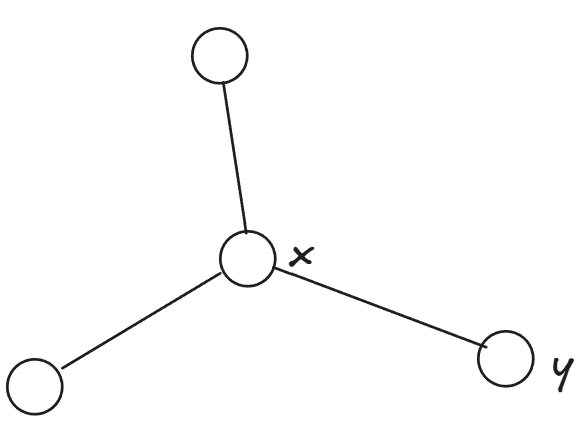
2. 若 $x$、$y$ 之间存在 $2$ 条或 $2$ 条以上的简单路径。因为 $x$、$y$ 之间无环，那么任意两条路径都至少有一个 $x$、$y$ 之外的交点。
   如果 $x$、$y$ 之间只有两条路径，那么两条路径的交点 $p$ 是割点，与图为 ”点双连通图“ 矛盾。
   如果 $x$、$y$ 之间有更多的路径，若这些路径都经过点 $p$，那么 $p$ 是割点，如果不经过点 $p$，那么这些路径两两相交，会形成一个简单环。

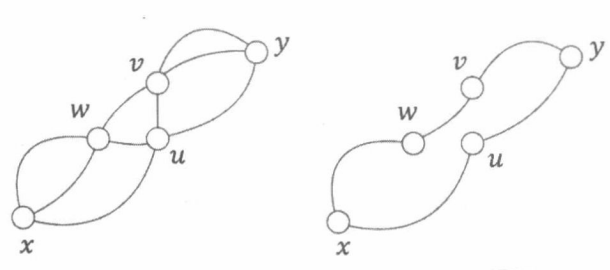
综上，任意两点均在一个简单环中。

点双连通分量

tip

无向图的极大点双连通子图被称为 ”点双连通分量“，简记为 ”v-DCC“（edge double connected component）。

1. 孤立点本身构成一个 v-DCC。
2. 割点可能属于多个 v-DCC，

点双连通分量的求法

为了求出 “点双连通分量”，需要在 Tarjan 算法中维护一个栈，并按照如下方法维护栈中的元素：

1. 当一个节点第一次被访问时，把该节点入栈。1
2. 当割点判定法则中的条件 $dfn[x] \le low[y]$ 成立时，无论 $x$ 是否为根，都要：
   1. 从栈顶不断弹出节点，直到节点 $y$ 被弹出。
   2. 刚才弹出的所有节点与节点 $x$ 一起构成了一个 v-DCC。

void tarjan(int x) {
    dfn[x] = low[x] = ++num;
    stack[++top] = x;
    
    if (x == root && head[x] == 0) { // 孤立点
        dcc[++cnt].push_back(x);
        return;
    }

    int flag = 0;
    for (int i = head[x]; i; i = Next[i]) {
        int y = ver[i];
        if (!dfn[y]) {
            tarjan(y);
            low[x] = min(low[x], low[y]);
            
            if (low[y] >= dfn[x]) {
                flag++;
                if (x != root || flag > 1) cut[x] = true;
                
                cnt++;
                int z;
                do {
                    z = stack[top--];
                    dcc[cnt].push_back(z);
                } while (z != y);
                dcc[cnt].push_back(x);
            }
        } else low[x] = min(low[x], dfn[y]);
    }
}

v-DCC 的缩点

v-DCC 的缩点比 e-DCC 要复杂一些——因为一个割点可能属于多个 v-DCC。设图中共有 $p$ 个割点和 $t$ 个 v-DCC。我们建立一张包含 $p+t$ 个节点的新图，把每个 v-DCC 和每个割点都作为新图中的节点，并在每个割点与包含它的所有 v-DCC 之间连边。 容易发现，这张新图其实是一棵树（或森林），如下图所示：

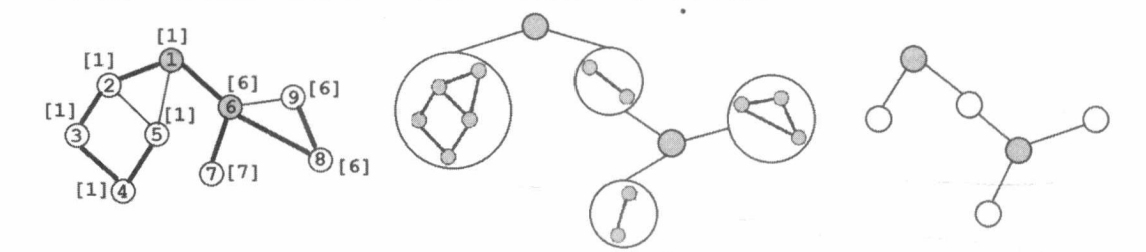
下面的代码在 Tarjan 求割点和 v-DCC 的参考程序的 main 函数基础上，对 v-DCC 缩点，构成一棵新的树（或森林），存储在另一个邻接表中。

// 给每个割点一个新的编号(编号从 cnt+1 开始)
num = cnt;
for (int i = 1; i <= n; i++)
    if (cut[i]) new_id[i] = ++num;

// 建新图,从每个 v-DCC 到它包含的所有割点连边
tc = 1;
for (int i = 1; i <= cnt; i++)
    for (int j = 0; j < dcc[i].size(); j++) {
        int x = dcc[i][j];
        if (cut[x]) {
            add_c(i, new_id[x]);
            add_c(new_id[x], i);
        }
        else c[x] = i; // 除割点外,其他点仅属于 1 个 v-DCC
    }

printf("缩点之后的森林,点数 %d,边数 %d\n", num, tc / 2);
printf("编号 1~%d 的为原图的 v-DCC, 编号 >%d 的为原图割点\n", cnt, cnt);
for (int i = 2; i < tc; i += 2)
    printf("%d %d\n", vc[i ^ 1], vc[i]);

相关题目

例1 Network

Network

给定一张 $N$ 个点 $M$ 条边的无向连通图，然后执行 $Q$ 次操作，每次向图中添加一条边，并且询问当前无向图中“桥”的数量。

题目需要求桥的数量，我们利用 Tarjan 算法求出图的所有 边双连通分量（e-DCC），并对每个 e-DCC 缩点，得到一棵树，树上的每个节点都对应原图的一个 e-DCC。设 $c[x]$ 表示节点 $x$ 所在的 e-DCC 的编号。最开始，桥 的总数就是缩点之后树的边数。

添加边 $(x, y)$ 后：

• 若 $(x, y)$ 属于同一个 e-DCC，则加边不影响桥的数量。
• 若 $(x, y)$ 属于不同的 e-DCC，则在缩点后得到的树上，$c[x]$ 与 $c[y]$ 之间的路径上的每条边都不再是 桥，从 $c[x]$、 $c[y]$ 向根节点方向移动，直到相遇，经过的边都标记为 “不再是桥”。若有 cnt 条边获得了标记，则把图中 桥 的总数减掉 cnt 即可。

上面算法执行 tarjan 和缩点的时间复杂度为 $O(n + m)$。执行查询操作的时间复杂度为 $O(qn)$。总共时间复杂度为 $O(m + qn)$。